“ le véritable voyage de découverte ne consiste pas à chercher de nouveaux paysages, mais à avoir de nouveaux yeux”
Marcel Proust
Cette semaine, Wonderful-art vous propose un voyage au cœur de l’harmonie et du sacré. Là où la pensée mathématique et la création se croisent pour parvenir à une harmonie sacrée .
Nous vous proposons de comprendre comment les propriétés fabuleuses du nombre d’or ont été découvertes et les créations qui en ont découlées. Comment une simple formule mathématique a t-elle pu donner une des clés pour comprendre l’harmonie sacrée qui régit à la fois la nature, la science et l’art?
La pensée mathématique :
Depuis la nuit des temps, l’Homme a cherché à comprendre son environnement, l’univers qui l’entoure. Le lien unique qui réunit toutes choses.
Il en rendra compte, d’abord , de manière symbolique (l’art), puis en inventant des langages ( l’écriture et la parole) afin de donner corps à ses observations et exprimer sous des formes diverses, des vérités existentielles profondes.
Le langage mathématique englobe à la fois des applications concrètes et symboliques. Il permet de mettre des mots sur ce que, jusqu’alors, seul l’art pouvait montrer et que le langage ne pouvait encore décrire. De cette pensée naîtra un éclairage nouveau sur le questionnement séculaire des causalités et des proportions.
Tablette de Plimton ( –1800 av JC) : servant à résoudre les problèmes calculatoires
Dans un premier temps les chiffres servent alors à révéler les interactions mystiques et les harmonies célestes. Le langage mathématique permet de mettre à jour les secrets les plus opaques… De ce nouveau champ d’application, le nombre d’or se révèle de manière concrète, libéré du sceau de l’abstraction et du mysticisme en permettant à l’Homme de découvrir toutes ces fabuleuses propriétés.
Bien qu’il fut compris bien avant, c’est à Euclide d’Alexandrie
(vers 325 – 265 av JC) dans l’ouvrage Eléments que nous devons la première “articulation” mathématique du nombre d’or.
Euclide dans son cinquième chapitre trace une ligne droite et la divise entre “extrême et moyenne raison”
On dit d’une droite qu’elle est partagée entre extrême et moyenne raison lorsque le rapport de la ligne entière à son segment le plus grand est égal au rapport de ce plus grand segment au plus petit.
C’est à dire AB/AC= AC/CB , AB est à AC ce que AC est à CB
Euclide inaugure dans son ouvrage “Eléments” un nouveau mode de pensée, basée sur la réflexion empirique permettant ainsi, de traduire la logique en langage compréhensible, afin d’en tirer des lois jusque là méconnues.
Le nombre d’or s’inscrit dorénavant dans cette aventure fabuleuse que d’autre après lui, continueront d’écrire au fil du temps.
La divine proportion :
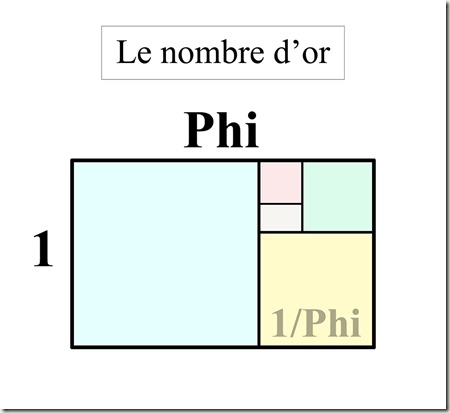
Découvert et redécouvert au fil des siècles, le nombre d’or est présent sous diverses nominations qui reflètent ses incroyables propriétés : la divine proportion, la division sacrée, le rapport doré, la section dorée, le nombre d’or… Toutes ces dénominations se réfèrent au rapport mathématique désigné par Phi.
Différentes appellations du Nombre d’Or :
1 – Nombre scandaleux car irrationnel (Platon)
2 – Proportion d’extrême et moyenne raison (Euclide)
3 – Proportion d’Euclide (Fibonacci)
4 – Section dorée (sectio aurea, Vinci)
5 – Divine proportion (selon Pacioli)
6 – Section d’or (der goldene Schnitt, Zeising)
7 – Nombre d’Or (fixé par Ghyka)
8 – Phi ( φ – expression mathématique, Mark Barr)
9 – Proportion dorée (selon l’usage courant)
anglais : Golden ratio – allemand : Der goldene Schnitt
Phi* est la relation, dans une proportion parfaite, du tout aux parties qui les composent.
Si la section dorée détient le pouvoir de créer l’harmonie, c’est en vertu de sa capacité sans pareil à unifier les différentes composantes d’un ensemble, de telle manière que chacune préserve son identité et parvient pourtant à se fondre dans la figure supérieure d’un ensemble singulier.
Gyorgy Doczy, Le pouvoir des limites
Bien qu’aujourd’hui, il nous semble qu’il ait toujours existé, soit en mathématique ou dans la nature, l’apparition du rapport du nombre d’or reste toutefois un mystère.
Les textes d’Erodote, le tout premier historien, au Ve siècle av. JC, laisse à penser que les égyptiens utilisèrent le nombre d’or pour construire la Grande pyramide, et que les grecs ont construit le Parthénon en se servant de “la section dorée”.
Bien qu’aucunes de ses créations n’aient traversées le temps, nous savons grâce à ceux que d’autres ont écrit, que le sculpteur et mathématicien Phidias (490 -430 av. JC) étudia la “section dorée” et l’appliqua aux ornements qu’il réalisa pour le Parthénon. La statue de Zeus à Olympie, son chef d’œuvre le plus célèbre, était l’une des Sept Merveilles du monde antique.
Héliogravure du “Voyage aux sept merveilles du monde” d’Augé de lassus (1880)
Platon (vers 427 – 347 av. JC), évoque aussi l’existence d’une proportion, connue aujourd’hui sous le nom de “juste milieu”, dans ses travaux sur les sciences naturelles et la cosmologie.
Par la suite, Euclide (325 – 265 av. JC) le traduira en langage mathématique grâce à son théorème et à sa démonstration, comme nous l’avons vu précédemment.
C’est au Moyen Âge, qu’un nouvel élan est donné au nombre d’or.
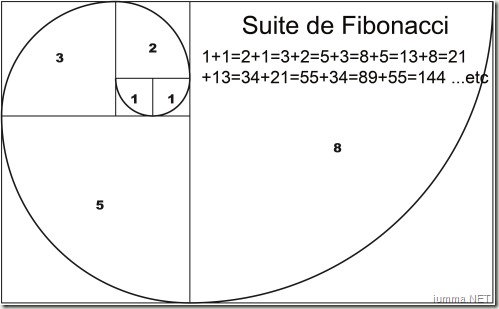
Léonard De Pise (1170-1250), plus connu sous le nom de Fibonacci, découvre les propriétés surprenantes d’une suite numérique qui porte son nom. Sa curiosité et son génie, lui ont permis de rassembler une masse d’information issue des connaissances des grecs qui, jusque là, échappait à l’Europe du Moyen Âge. Toutefois, on ignore si ce dernier avait vu la correspondance entre sa découverte et le nombre d’or.
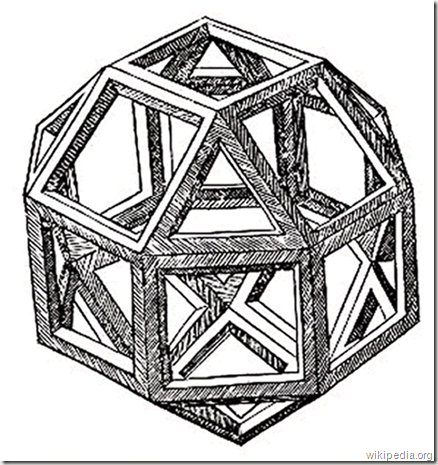
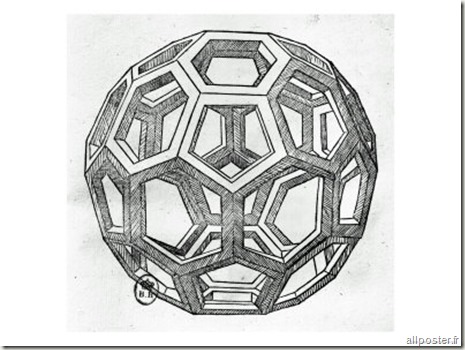
Luca Pacioli (1445 – 1517), géomètre, redécouvrit le “secret d’or” et le nomma “divine proportion” dans le traité du même nom publié en 1509. Ami des grands peintres de la renaissance, c’est Léonard de Vinci qui illustra cet ouvrage avec entre autre, les fabuleux dessins des cinq solides de Platon.
C’est sans doute Léonard de Vinci qui fut le premier à parler de “sectio aurea” ou section dorée.
C’est dans leur soif d’harmonie, de symétrie et d’équilibre de la beauté que les sculpteurs, architectes et les peintres de la Renaissance et de l’antiquité, furent nombreux à utiliser le nombre d’or.
Le nombre d’or et ses ramifications dans d’autres domaines.
“Une gamme de proportions qui rend le mal difficile et le bien facile”
Albert Einstein (commentaire sur l’invention du modulor par Le Corbusier)
Johannes Kepler (1571 – 1630), mit en évidence la correspondance entre le nombre d’or et la suite de Fibonacci. Son étude des plantes, l’amène à penser que cette séquence se retrouve dans la croissance végétale.
C’est à Mark Barr que l’on doit, en 1929, la lettre grecque phi pour identifier la divine proportion, il renvoie à Phidias et au F du nom de Fibonacci.
Le physicien Roger Penrose, lui, fut connu pour sa découverte du “Pavage de Penrose”. Il permet de “paver” des surfaces en respectant un type de symétrie considérée alors comme impossible. Cette découverte décisive dans la compréhension de la matière, et la description des “quasi-cristaux”, permet de présenter des axes pentagonaux ou décagonaux tous liés au nombre d’or.
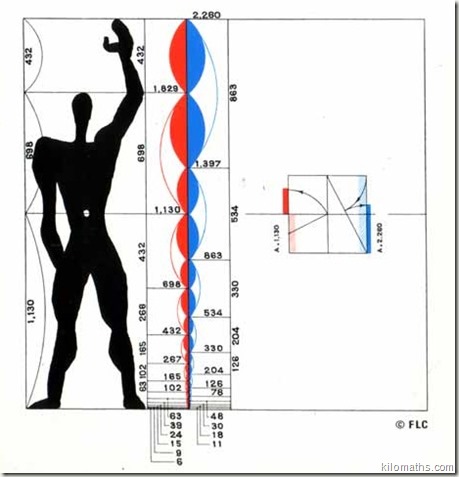
Le Corbusier inventa en 1943, un ensemble de mesure proportionnelle reposant sur les proportions du corps humain “ le modulor” afin de réconcilier la beauté du nombre d’or et les besoins du corps humain.
Nous pouvons nous rendre compte dans cette première approche sur l’histoire du nombre d’or et de ces quelques exemples d’applications non exhaustifs, combien cette formule a changé notre façon de penser, la vison de notre environnement, et notre façon de la retranscrire de manière compréhensible.
Combien cette recherche perpétuelle de l’harmonie, de la beauté, et de l’équilibre nous a conduit sous différente forme, dans la même direction pour devenir une évidence, qui suscite encore aujourd’hui tant de questions sans réponses. Tous ces chercheurs se rejoignent sur un point fondamental : la vie reste un mystère infini.
Sources :
– Le code secret, la formule mystérieuse qui régit les arts, la nature et les sciences . Priya Hemenway. édition Evergreen
– wikipédia













J’utilise régulièrement la suite de Fibonacci dans mon métier d’informaticien. Elle permet d’évaluer la complexité d’une tâche et est très utilisée dans la méthodologie « Agile »: http://fr.wikipedia.org/wiki/Planning_poker
Alors j’ai regardé le lien et j’ai rien compris lol ^^
Quel livre sans trop de mathématiques sur l histoire et les applications variées du nombre d or